Autism Spectrum Disorder, 2: Observations on the Imprecision of the Numerical Value of Risk when Examining Predictors of Risk in Regression

Autism spectrum disorder (ASD) is multifactorial in origin, with hundreds of genes and more than a hundred environmental exposures identified as potential causes, mediators, or markers of risk.¹ On the surface, risk is a concept that is easy to understand, and values of risk are easy to interpret.² What is less well recognized, however, is that although a value for risk, in any given study, is a definite number, the interpretation of this number can be nuanced. Knowing how to interpret this number, and how to recognize the limitations of the “definiteness” of this number, is important for understanding the field, for communication to patients in shared decision-making processes, for communication as teaching to peers and the public, and for policy framing.

This article explains the complexities of understanding risk in the context of antidepressant exposure during pregnancy as a risk factor for ASD. This context has been chosen merely as an example; much of the discussion that follows applies to other risk factors for ASD in other contexts, and to other risk factors for other outcomes, as well.

The initial sections of this article cover basic territory. More knowledgeable readers may wish to skip these sections.

Introductory Notes: Research Design

Does gestational exposure to antidepressant drugs increase the risk of ASD in offspring? This is a research question that is ideally answered in randomized controlled trials (RCTs), a research design that generates the highest quality of evidence. However, RCTs are time-consuming, labor-intensive, and expensive to conduct. For some research questions, such as those with infrequent outcomes (ASD is an example), an adequately powered RCT could require several thousand subjects; and in some contexts (pregnancy is an example), conducting an RCT could be ethically challenging. So, for many research questions, we may need to look at observational studies, such as cohort and case-control studies, to learn about risks.

Epidemiological Data: Crude Values

In observational studies, crude epidemiological data, such as the incidence of an adverse outcome, can convey an idea about risk in exposed vs unexposed groups. For example, Hagberg et al³ found that the incidence of ASD was 1.73% vs 0.97% in offspring with vs without gestational exposure to antidepressants. This suggests that antidepressant exposure increased the risk by 0.76%, or that the crude number needed to harm is 132.

The observed values and calculations based directly thereon are called crude because they have not been adjusted for biases. The importance of differentiation between crude and adjusted values is explained in later sections of this article.

Measures of Effect Size: Crude Estimates

In observational studies, measures of effect size, such as the odds ratio (OR), are usually obtained. As examples, in a study by Rai et al,⁴ the crude OR was 1.47, suggesting that gestational exposure to antidepressants increased the risk of ASD in offspring by approximately 47%. In another study,⁵ the crude hazard ratio (HR) was 1.51, suggesting that first trimester gestational exposure to antidepressants increased the risk of ASD in offspring by approximately 51%.

As a digression, the OR and the HR in the examples above were interpreted as though they were relative risks (RRs). ORs and HRs are not the same as RRs either conceptually or numerically. Nevertheless, there are certain circumstances, but certainly not all circumstances, in which ORs and HRs can be interpreted as RRs. These are explained in Boxes 1 and 2. The reader would need to exercise judgment on a case-by-case basis when interpreting ORs and HRs as RRs.

Again as a digression, the OR in case-control designs does not estimate the risk of outcome in exposed vs unexposed individuals; rather, it estimates the risk of exposure in individuals with vs without the outcome.⁶ Thus, in such studies, the OR is not only numerically but also conceptually different from the RR.⁷ The difference can be large for outcomes that are common in the population.⁶

The Limitation and Usefulness of Crude Values

Crude values straightaway give us an idea about absolute and relative risks in the real world. However, crude values are biased estimates. Consider that, as already noted, hundreds of genes and environmental exposures have been associated with increased risk of ASD.¹ In RCTs, we could expect these risks to be reasonably balanced between antidepressant-exposed and antidepressant-unexposed groups. In observational studies, however, the exposed group is more likely to be loaded for risk factors than the unexposed group. For example, in the study by Boukhris et al,⁵ women who used antidepressants during pregnancy were more likely to have diabetes and hypertension, and their offspring were more likely to have low birth weight.

So, if we merely look at the crude values for incidence, number needed to harm (NNH), and OR, we run the risk of attributing to antidepressant exposure not only the risk (if any) associated with antidepressant exposure but also the risks associated with the extra risk factors, such as those referred to in the previous paragraph.

For this reason, investigators do not consider crude values in evaluating cause-effect relationships and in decision-making processes; rather, they use models of regression, such as logistic regression or Cox proportional hazards regression, to mathematically identify the unique contribution of antidepressant exposure that remains after mathematically adjusting for the contributions of the other risk factors. The variables adjusted for are called covariates or confounds, depending on their relationships with the exposure of interest and the outcome of interest.⁸ Once we know, from the regression, what the unique contribution of antidepressant exposure is, we can, perhaps, more confidently communicate to women about the extent to which gestational antidepressant exposure may increase the risk of ASD in offspring.

Note that this does not mean that crude values are useless. Because crude values provide information about what might happen in the average patient in the real world, they are helpful to guide expectations and plan clinical care. So, if crude values suggest that gestational exposure to antidepressants increases the risk of various pregnancy, fetal, neonatal, and childhood adverse outcomes, we would counsel women and plan clinical care accordingly even if we know that the antidepressant exposure may be merely a marker of risk and not causal for the adverse outcomes.

Single Studies vs Meta-Analysis

A single, large, well conducted and well-analyzed study with good control for confounding trumps meta-analysis if most or all of the other studies in the meta-analysis are small, poorly conducted, poorly analyzed, poorly adjusted for confounds, and poor in quality. Nevertheless, especially with regard to observational research, it is best to examine results from meta analyses, if these are available. This is because meta-analysis results are based on a larger (pooled) sample, because biases of the estimate of interest in individual studies will hopefully be scattered uniformly around the pooled estimate, and because representation of diverse samples in the meta-analysis will improve the generalizability of the pooled estimate. However, in some circumstances, an individual patient’s needs might be better served by consulting a single, good, and particularly representative study, and so, in such circumstances, clinicians should exercise their judgment in deciding what to consult.

Despite best efforts, observational studies are inevitably undermined by inadequately measured, unmeasured, and unknown confounds. Meta-analysis does not remove these confounds; when estimates from individual studies are biased by confounds, the pooled estimate in meta-analysis will also be biased by confounds. So, numerical values for risk obtained in meta-analyses of observational data are also subject to the uncertainties discussed in later sections of this article.

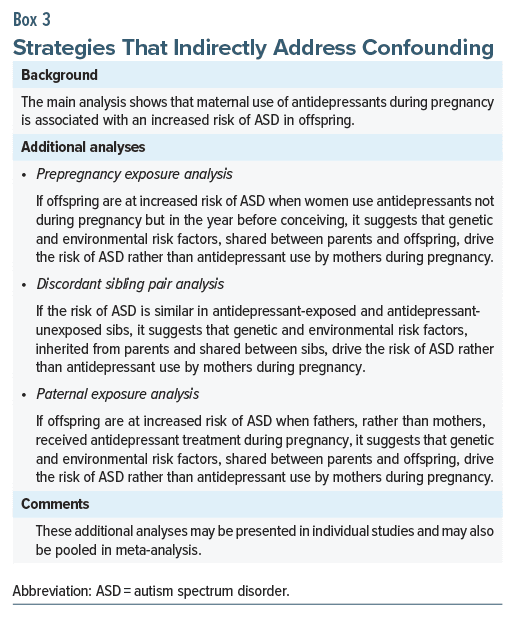
Strategies That Indirectly Address Confounding

If confounding is inevitable in observational studies, it is desirable to first examine results from analyses that innovatively get around the confounds. With reference to the risk of ASD in offspring gestationally exposed to antidepressants, we need to adjust for the many genetic and environmental risk factors that have been associated with ASD.¹ However, information about such exposures will not be available in the healthcare databases from which study data are sourced, even if we are confident about the identity of the exposures that we need to adjust for. In this context, there are 3 strategies that can indirectly reduce confounding by unmeasured and even unknown genetic and environmental risk factors. These strategies are analysis of outcomes associated with prepregnancy exposure, discordant sibling pair analysis, and analysis of outcomes associated with paternal exposure; the latter 2 strategies were discussed in earlier articles in this column.^1,9 Explanations are provided in Box 3.

If strategies that address confounding, such as those presented in Box 3, suggest that shared genetic and environmental factors explain the risk of ASD in offspring, then the value of the adjusted risk estimate for antidepressant exposure, obtained in regression, is merely of academic interest (but, as explained earlier, we continue to be interested in the crude risk). This is because, regardless of its statistical significance, the adjusted risk estimate for antidepressant exposure probably does not indicate a cause-effect relationship and so there is little to be gained in trying to quantify its “unique contribution” to the outcome in multivariable regression.

The Numerical Value of the Adjusted Risk Estimate

Consider a fictitious case-control study in which gestational exposure to antidepressant drugs was compared between children with ASD and a randomly selected age- and sex-matched sample of children without ASD. The crude OR associating antidepressant exposure with ASD was 2.00 (95% confidence interval [CI], 1.21–3.33). After adjusting for maternal sociodemographic variables, maternal medical health variables, and maternal use of other drugs during pregnancy, the adjusted OR (aOR) was 1.50 (95% CI, 1.05–2.15). The prevalence of ASD among young children was 2.5% in the healthcare database from which the study data were extracted.

The conventional way in which the findings of this fictitious study are interpreted and communicated is presented in Box 4. All 4 statements in Box 4 are wrong to varying extents. Here is why.

Statement 1 is wrong because this was a case-control study, and an OR obtained from a case-control study is conceptually and numerically not the same as an OR obtained from a cohort study. This was explained in an earlier article in this column.⁷

Statement 2 is true for the average woman who is considering antidepressant treatment during pregnancy but may be wrong for an individual woman because she may not be average; what her child’s risk is would depend on the other covariates and confounds to which she is exposed. Readers can obtain an idea of how much this woman differs from the average by examining the study descriptive statistics that compare exposed and unexposed women. This information is usually presented as Table 1 in a paper. Readers are reminded that this table presents data on only measured variables. There are likely to be unmeasured and unknown variables that also influence the outcome, making it impossible to truly determine how average an individual patient is. Readers may also note that if a woman is sampled from another population, the applicability of the study findings to that woman will depend on the generalizability of the study findings to that population.

Statement 3 is wrong for several reasons. First, the true value of the aOR may differ from 1.50; all relevant covariates and confounds have not been adjusted for. Examples of such covariates and confounds include smoking, drinking, use of illicit drugs, exposure to environmental toxins, and maternal depression and the severity thereof. The value may increase or decrease with the addition of covariates, depending on how these covariates correlate with the exposure (resulting in decrease) and explain additional variance in the outcome (resulting in increase). The value will decrease when adjusting for confounding.¹⁰ Second, the aOR does not represent a unique contribution; rather, it is the contribution of the antidepressant exposure plus residual confounding from the unmeasured and unknown confounds that were not adjusted for in the regression. Interpreting the aOR is especially wrong if the unique contribution is viewed as cause and effect (Box 5).

Third, and this is particularly important, Statement 3 is true only for the average woman in the sample who has an average set of risk factors for ASD. It is not true for a specific patient because we cannot assume that this patient is an average woman. Therefore, a 50% increased risk refers not to a 50% increase over the ASD base rate among offspring in the whole sample (or population) but a 50% increase in the ASD base rate among offspring of other women in the study sample with this patient’s set of risk factors (Box 5).

Statement 4, as explained in the previous paragraph, is true only for the average woman in the sample who has an average set of risk factors for ASD. It is not true for a specific patient whose set of risk factors differ from the average in the sample.

Approaches to Analysis

In observational studies, ORs obtained in analyses of subsamples created by propensity score-matching will not apply to the full sample, let alone to the population. Propensity score matching improves internal validity but compromises external validity much the same as narrow sample selection criteria do in RCTs. Generalizability from propensity score-matching analyses can be improved, for example, by using the propensity score as a covariate in a regression conducted on the full sample; that is, the propensity score is used to adjust for treatment bias arising from measured covariates. Analysis may also be conducted on the full sample after inverse probability of treatment weighting (IPTW) using propensity scores based on measured covariates. However, IPTW changes the characteristics of the sample that is being analyzed and improves the internal validity of the analysis, but not the external validity.

The observations made here refer to the value of the OR and not to the validity of the findings of the different approaches to analysis. It must be remembered that, in these analyses as well, the value of the OR and the validity of the findings both remain compromised by residual confounding.

Using the Regression Equation

Instead of approximating the risk of offspring ASD using the sample OR, can the regression equation, generated during analysis, be used to calculate a precise value for risk in an individual patient who needs to decide whether or not to accept antidepressant treatment during pregnancy? Yes, certainly; but only if the regression equation was obtained in its simplest multivariable form; if advanced statistical models of regression were used, then the applicability of that equation to an individual patient would depend on the model of regression and the way in which the weights were derived. A discussion on this subject is beyond the scope of the present article.

A point is made here that calculating a patient’s risk manually using the full regression equation with the weights for all covariates is problematic if the patient who is being assessed does not belong to the same population as that from which the regression sample was drawn; if data for all covariates in the equation are unavailable for the patient; if the regression was performed on a modified sample, such as in patients who were propensity score-matched for antidepressant treatment vs no treatment; and if the regression equation was not validated, such as in a separate sample.

Using the regression equation to calculate an individual patient’s risk is also problematic for 2 more reasons. One is that study results that are published do not include detailed information about the covariates in the equation, their coding, and their regression weights. The other is that even if all the requirements listed in this section are met, the regression does not include unmeasured and unknown confounds, and it would not be correct to assume that the set of these unmeasured and unknown confounds would be the same in the patient being assessed as in the average patient in the sample in which the regression was derived.

Readers are reminded here that there are dozens of potentially measurable risk factors for ASD¹ for which information is unavailable in the databases from which information is drawn for antidepressant-pregnancy-offspring ASD observational studies. The regression equation is incomplete when these risk factors are not included.

Simultaneous Presence of Many Risk Factors

As repeatedly observed, gestational exposures to a very large number of risk factors have been associated with an increased risk of ASD in offspring.¹ The statistically significant ORs/RRs for some risk factors have been low to modest; for example, 1.09 for antibiotics,¹¹ 1.32 for maternal infection/fever,¹² 1.40 for maternal polycystic ovarian disease,¹³ 1.44 for maternal anemia,¹⁴ 1.48 for maternal diabetes,¹⁵ and 1.51 for greater paternal age.¹⁶ The ORs/RRs for other risk factors have been high to very high; for example, 2.52 for professionally applied indoor insecticides,¹⁷ 3.02 for cannabis use disorder,¹⁸ and 4.19 for valproate.¹⁹

Many of the gestational exposures identified as risk factors,¹ such as obesity, polycystic ovaries, hyperemesis, infection/fever, antibiotic/paracetamol use, and obstetric complications, are common, and so an individual woman is likely to have exposure to several of these common risk factors in any given pregnancy. Such women come to attention when, for example, they need treatment with an antidepressant drug for depression during pregnancy. When counseling such women about risks, we need to consider what might be the impact of exposure to many ASD risk factors in addition to the potential risks associated with exposure to depression and to antidepressant use.

Assume that we know all the risk factors to which the woman is exposed. If these risk factors are completely independent of each other, then the overall risk of offspring ASD is the product of the individual risks. As an example, if a woman is exposed to 6 risk factors each of which increases the risk of ASD by about 50% (OR, RR, or HR approximately 1.50), then the overall risk is 1.5 multiplied by itself 6 times; that is, the child’s risk of ASD is approximately 11 times whatever the base rate might be. So, if the hypothetical base rate is 2%, the child’s risk of ASD is a staggering 22%.

If only 3 risk factors are present, and this is a reasonable possibility, given how common most of the risk factors are, with the same assumptions as in the previous paragraph, we estimate that the child’s risk of ASD is about 6%–7%. We know that the incidence of ASD is increasing and that many explanations have been suggested¹; however, the current incidence of ASD in the general population is far short of 6%–7%. So, why don’t the numbers reflect what we see?

Risk Factors May Not Be Independent of Each Other

A possibility to be considered is that, in the real world, many of the risk factors are not independent of each other; that is, the risk factors are correlated with each other to a small or large extent. As an obvious example, gestational exposure to maternal infection, maternal fever, maternal use of antibiotics, maternal use of paracetamol, changes in maternal levels of immune and inflammatory molecules, and changes in the maternal gut microbiome have, in separate studies (hence, with adjustment for separate sets of covariates), each been associated with ASD risk in offspring¹; but a moment’s reflection will tell us that a woman who experiences one of these exposures might also experience some or all of the rest. In fact, an examination of the many dozens of risk factors identified for ASD¹ would reveal that many such sets of risks can be identified.

The implication is that when risk factors move in sets, they may behave like a single risk factor which may describe only a small increase in the risk of the outcome relative to the individual risk factors in the set. So, the true risk of offspring ASD associated with exposure to multiple risk factors may be much lower than that calculated as shown in the preceding section.

The Elephant in the Room

We have already seen that there are many reasons why the value of the aOR and its impact on the absolute risk for an individual patient are not numbers that are set in stone. However, and this is rarely expressed, there is another important but little understood reason why the value of the aOR may be a blurred concept.

Consider a hypothetical situation. There are a dozen and more strategies that could improve a young woman’s 100 m sprint timing. As examples, she could sleep optimally, eat optimally, drink coffee, wear special shoes, wear special clothing, run on a synthetic track, and be chased by a bull; but, even though each of these could meaningfully improve her timing, and even though each of these is independent of the rest, using all these strategies together might not do much more than any one of the strategies applied alone. And it is almost certain that, no matter how much she trains, she will never run the 100 m in <10.5 s. A likely explanation is that even if the running strategies differ in proximal mechanisms, they converge in eventual mechanisms, and that convergence may saturate; so, adding strategies does nothing more.

In like manner, it is theoretically possible that the presence of many environmental risk factors for ASD may not result in a multiplied or even a merely moderately magnified risk even when the risk factors are independent of each other. This is possible if the different risk factors, though statistically independent (uncorrelated), act through similar distal mechanisms, and if the distal mechanisms can be saturated; so, adding more risk factors will not increase the risk because the mechanisms that lead to ASD are already saturated. If this is true, it could explain why the population prevalence of ASD is still in the 2%–3% range although the risk factors for the disorder are very many, although many of these risk factors are common, and although many of these risk factors are each associated with at least a moderate increase in risk.

As a spin-off, this could mean that the real potential of a risk factor and its so-called unique effect identified in regression are not the same. In fact, if many risk factors are adjusted for in multivariable regression, even if each truly explains a substantial and statistically significant proportion of the variance in the outcome (as identified in independent studies), if they act through common mechanisms that saturate, their unique contributions (and the value of the associated aORs) could be (falsely) small and statistically not significant.

So, in the context of an individual who is being counseled, the true potential or numerical value of the risk could depend on what other risk factors are present and the extent to which those risk factors saturate mechanisms for the outcome of interest. If other risk factors are few, saturation of mechanisms may be less, and the value of risk (for the risk factor of interest) might be found to be larger than the value identified as the unique effect when the other risk factors are present.

Expressed differently, the elephant in the room is that in a study of, for example, gestational exposure to a risk factor and ASD risk in offspring, how do we know to what extent other risk factors in the regression are saturating the pathways leading to ASD, thereby decreasing the value and statistical significance of the aOR of the risk factor of interest?

Take-Home Message

The value of an estimate of risk in a regression is not set in stone. It is heavily nuanced by considerations that include the nature of the sample and the biases contained therein, the covariates and confounds that are and are not adjusted for in analysis, the interactions between the exposure and the other variables, the extent to which exposures saturate downstream mechanisms, and the nature of the analysis, itself. Because, as discussed in this article, the nature and magnitude of these considerations are context-specific, when we view the value of and confidence interval around a risk estimate, our understanding of and communication about the risk estimate must be nuanced and context-specific.

Readers who are dismayed by this uncertainty should remember that, for example, response and remission rates obtained from RCTs and meta-analyses of RCTs are much simpler to understand but also depend on context and are not set in stone.

Parting Note

Readers interested in uncertainty of risk estimates arising in a different context, from clinical prediction models, may refer to the discussion by Riley et al.²⁰

Article Information

Published Online: May 14, 2025. https://doi.org/10.4088/JCP.25f15918
© 2025 Physicians Postgraduate Press, Inc.
To Cite: Andrade C. Autism spectrum disorder, 2: observations on the imprecision of the numerical value of risk when examining predictors of risk in regression. J Clin Psychiatry 2025;86(2):25f15918.
Author Affiliations: Department of Psychiatry, Kasturba Medical College, Manipal Academy of Higher Education, Manipal, India; Department of Clinical Psychopharmacology and Neurotoxicology, National Institute of Mental Health and Neurosciences, Bangalore, India.
Corresponding Author: Chittaranjan Andrade, MD, Department of Clinical Psychopharmacology and Neurotoxicology, National Institute of Mental Health and Neurosciences, Bangalore 560029, India ([email protected]).
Relevant Financial Relationships: None.
Funding/Support: None.