The results of research on a specific question differ across studies, some to a small extent and some to a large extent. Meta-analysis is a way to statistically combine and summarize the results of different studies so as to obtain a pooled or summary estimate that may better represent what is true in the population. Meta-analysis can be conducted for a variety of statistics, including means, mean differences, standardized mean differences, proportions, differences in proportions, relative risks, odds ratios, and others. The results of meta-analysis are presented in forest plots. This article explains why meta-analysis may be necessary, how a systematic review is conducted to identify studies for meta-analysis, and how to interpret the various elements in a forest plot. Brief discussions are provided about important concepts relevant to meta-analysis, including heterogeneity, subgroup analyses, sensitivity analyses, fixed effect and random effects meta-analyses, and the detection of publication bias. Other procedures briefly explained include meta-regression analysis, pooled analysis, individual participant data meta-analysis, and network meta-analysis. The limitations of meta-analysis are also discussed.

ABSTRACT
The results of research on a specific question differ across studies, some to a small extent and some to a large extent. Meta-analysis is a way to statistically combine and summarize the results of different studies so as to obtain a pooled or summary estimate that may better represent what is true in the population. Meta-analysis can be conducted for a variety of statistics, including means, mean differences, standardized mean differences, proportions, differences in proportions, relative risks, odds ratios, and others. The results of meta-analysis are presented in forest plots. This article explains why meta-analysis may be necessary, how a systematic review is conducted to identify studies for meta-analysis, and how to interpret the various elements in a forest plot. Brief discussions are provided about important concepts relevant to meta-analysis, including heterogeneity, subgroup analyses, sensitivity analyses, fixed effect and random effects meta-analyses, and the detection of publication bias. Other procedures briefly explained include meta-regression analysis, pooled analysis, individual participant data meta-analysis, and network meta-analysis. The limitations of meta-analysis are also discussed.
J Clin Psychiatry 2020;81(5):20f13698
To cite: Andrade C. Understanding the basics of meta-analysis and how to read a forest plot: as simple as it gets. J Clin Psychiatry. 2020;81(5):20f13698.
To share: https://doi.org/10.4088/JCP.20f13698
© Copyright 2020 Physicians Postgraduate Press, Inc.
A magnetic resonance imaging (MRI) study conducted in alcoholic men and women found that adverse brain findings were greater in men than in women.1 Another MRI study of alcoholic men and women, published as the next article in the same issue of the same journal, found that the adverse brain findings were greater in women than in men.2 The findings in each study were true for the sample, but what is true for the population? Is one sex more vulnerable to the neurotoxic effects of alcohol and, if yes, which sex?
One way of resolving the issue is to conduct further studies. However, what if the new studies fail to provide a consensus? Would a qualitative review of the research, conducted by experts in the field, resolve conflicts? Not necessarily. For example, 2 expert reviews published at around the same time reached contrasting conclusions about the safety of continuing lithium during a course of electroconvulsive therapy.3,4 Vote counting is also no solution. Five studies may obtain a particular result, but if these 5 studies have small samples and are poorly conducted, a large and methodologically more rigorous study may be more trustworthy even if its findings are different from those previously obtained.
This article introduces meta-analysis and concepts related thereto. The presentation has been made simple, but readers will nevertheless need to have some background knowledge of certain statistical concepts. For readers who do not have the necessary grounding, references are provided in the relevant places.
Need for Meta-Analysis
Meta-analysis is a procedure that mathematically combines and summarizes the results for a specific outcome, as extracted from several similar empirical studies. Meta-analytic methods were used as far back as in the 1930s, but the term meta-analysis was coined much later, by Glass, in 1976. The procedure became popular after it was used to synthesize outcomes from psychotherapy and counseling studies.5-7 There are at least 3 kinds of situation in which meta-analysis may be applied.
When several studies throw up a mixed bag of findings, some “positive” and some “negative,” meta-analysis can provide an objective average that dispenses with the need for expert opinion and vote counting. For example, out of 33 randomized controlled trials (RCTs; pooled N = 36,974) that were conducted between 1959 and 1998, 5 found that intravenous streptokinase significantly reduced mortality in patients with acute myocardial infarction, another 20 found an advantage for streptokinase that did not reach statistical significance, and a further 8 found that streptokinase was associated with worse outcomes than control treatment, though not significantly so. In meta-analysis, the advantage for streptokinase was consistently statistically significant by 1973, itself; specifically, from the eighth trial (pooled N = 2,432) onward. Subsequent trials made the pooled estimate more precise but negligibly altered its value.8 Very obviously, a lot of RCTs were unnecessarily performed, and many lives could have been saved had meta-analysis been applied to the data earlier.
When several small studies find that the results are “positive” but mostly do not reach “statistical significance,” pooling results in meta-analysis provides a larger sample size, based on which it becomes easier to identify statistical significance. For example, 5 of 6 RCTs found that modafinil or armodafinil were nonsignificantly better than placebo for the reduction of negative symptom severity in schizophrenia; a sixth RCT found a significant advantage for modafinil. When the RCTs were pooled in meta-analysis, a significant advantage was found, favoring modafinil/armodafinil.9
When several studies find that a result is “positive” and even “statistically significant,” meta-analysis can still be helpful, such as to determine how large the finding is, and to improve the precision of the estimate. For example, 8 RCTs all found intranasal esketamine to be superior to control treatment in patients with depression, and the meta-analysis provided a pooled estimate of the magnitude of the treatment effect.10
The Systematic Review
Data for meta-analysis are extracted from source studies conducted on the topic of interest. Authors who wish to perform a meta-analysis should not select their source studies based upon judgment, or upon published studies that they have come across during the course of their reading. Such meta-analyses would be biased by author opinions and would miss the contributions from source studies that the authors are unaware of. Source studies are therefore identified through a process that is known as a systematic review.
In a systematic review, the authors formulate a search strategy in advance. This primarily involves listing search terms and how these terms will be combined, as well as listing the electronic databases that will be searched using the search term combinations. Authors will typically also search for unpublished literature in clinical trial registries, for additional studies in the reference lists of identified literature, and for data available in conference abstracts. They may additionally search the contents of journals specifically related to the field and write to individuals and organizations that are involved in research on the subject. All search results are recorded.
The review protocol typically specifies criteria that would make identified studies eligible or ineligible for inclusion in the meta-analysis. For example, a meta-analysis on the efficacy of a drug may specify that only parallel group RCTs would be considered, and only if these RCTs use a specified minimum dose of the drug for a specified minimum duration in a specified diagnostic category of patients. Additionally, the source studies would be required to provide data on the outcomes of interest, and in a format that allows extraction for use in meta-analysis (when the data are unavailable, the meta-analysis authors will write to the source study authors to request the necessary data).
Searches are usually performed independently by 2 members of the meta-analysis team and the results are compared; differences in opinion are resolved by discussion and consensus or by arbitration by a third member of the team. This helps ensure that the search is complete and fair. The step-by-step results of the search, leading to the final list of studies for meta-analysis, are presented in a Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) flow diagram in the report that describes the meta-analysis.
Good meta-analyses are expected to be PRISMA-compliant in all regards (http://prisma-statement.org/); this includes the prospective registration of the study protocol with PROSPERO, an international registry of systematic reviews in health and social care.11
Study Scrutiny, Data Extraction, and Data Analysis
Studies that are shortlisted for meta-analysis are examined for risk of bias. Different instruments are available for this purpose; examples include the Jadad Scale for RCTs and the Newcastle-Ottawa Scale for nonrandomized studies such as cohort and case-control studies. As an example, with regard to RCTs, bias is assessed in several domains, including those related to randomization, blinding, occurrence of protocol deviations, handling of missing data, presence of selective outcome reporting, and others.12
Data from the source papers are usually independently extracted by 2 members of the team; the results are compared, and differences reconciled through discussion and arbitration, as discussed earlier. Analysis is performed using statistical software such as RevMan, which is available, free, at the Cochrane website. This website also provides online training in conducting systematic reviews and meta-analysis (https://training.cochrane.org/). The Cochrane Handbook for Systematic Reviews of Interventions, a bible of sorts for learning how to understand and perform meta-analysis, is also available free for readers who register at this website.
Summary Estimates
When values for a specified outcome are extracted from different studies and averaged in meta-analysis, the result is known as a pooled estimate or a summary estimate. Pooled estimates can be obtained for a variety of parameters, including means, mean differences (MDs) or weighted mean difference (WMDs), standardized mean differences (SMDs), proportions, differences in proportions, relative risks (RRs), odds ratios (ORs), and others. The pooled estimates are presented along with 95% confidence intervals (CIs). In order to better follow the rest of this article, readers would need to have a working understanding of these terms; explanations and discussions have been provided in earlier articles in this column.13-16
The Forest Plot: Overview
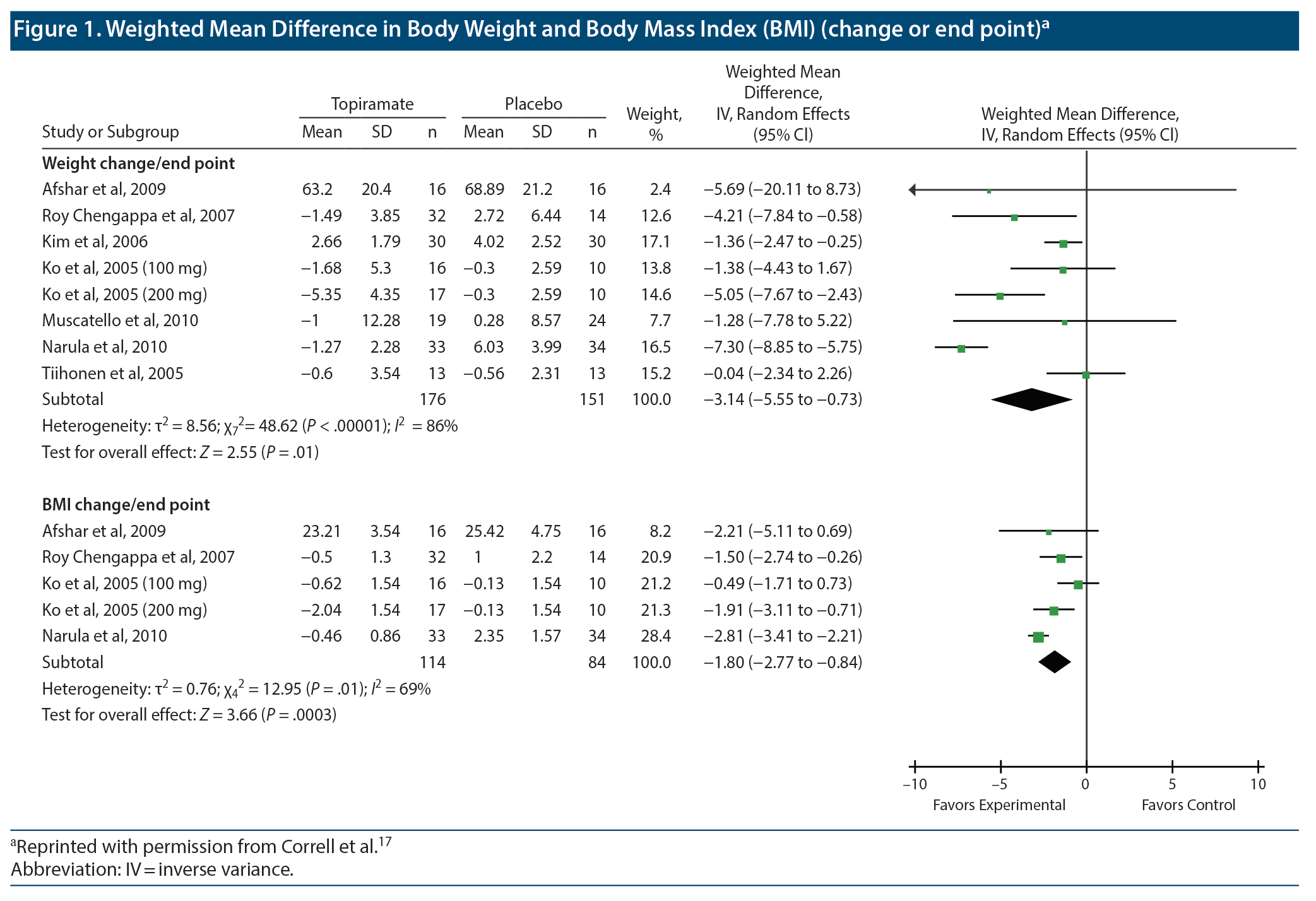
The main results of meta-analysis are presented in forest plots. Figure 1 and Figure 2 are examples of forest plots that have been reproduced (with permission) from a meta-analysis that pooled RCT data on benefits with topiramate augmentation of antipsychotic drugs in patients with schizophrenia spectrum disorders.17 The origin of this use of the word forest is not known for certain; it probably refers to the “forest” of lines displayed in the plot.
The title of the forest plot tells us what is presented in the plot. Thus, for example, we see that Figure 1 contains 2 forest plots; the upper plot presents WMD outcomes for weight and the lower plot presents WMD outcomes for body mass index (BMI).
As an aside, it is unlikely that patients’ heights would change during the course of a clinical trial, so why present data on both change in weight and change in BMI? The answer could be that some trials presented one and some presented the other. However, if this was so, the data could have been pooled as SMDs instead of as MDs.13 Furthermore, on comparing the upper and lower plots, it is apparent that all the studies that presented data on BMI also presented data on weight. An explanation for the apparent redundancy is that some readers may be interested in the BMI values because these are material to the definitions of overweight and obesity.
In Figure 1, in each forest plot the first column lists the RCTs that contributed data to the meta-analysis presented in the plot. Each study is listed as the first author’s last name and the year of publication of the study. The list of studies is usually presented in alphabetical order (as in Figure 1 and Figure 2), sometimes in chronological order, and rarely in the order of the effect size.18
In Figure 1, columns 2-4 present data for the topiramate arm, and columns 5-7 present data for the placebo arm in each RCT. The 3 topiramate columns and the 3 placebo columns present data on mean, standard deviation (SD), and sample size (n) for the respective treatment arms. The column headings are self-explanatory.
All studies do not contribute equally to the pooled estimate; in this regard, the weight assigned to each study is stated in column 8. The concept of weights in meta-analysis was explained in the previous article in this column.13 Column 9 carries a slightly misleading heading. A better heading would be “Mean Difference (95% CI)” and not what is actually stated. Why this is so will become apparent in the next section. The actual plot that presents the data in visual form is at the extreme right of the figure.
There are 3 rows at the bottom of each plot, below the study listings. These rows present the summary information and the meta-analysis results for the efficacy outcome that is the subject of the forest plot.
Study Data in the Forest Plot: 1
Let us examine the first source study in the upper forest plot that is presented in Figure 1. This study is listed as Afshar et al, 2009. There were 16 patients in each treatment arm (columns 4 and 7). At the study endpoint, the mean body weight was 63.20 kg in the topiramate arm (column 2) and 68.89 kg in the placebo arm (column 5). When we subtract 68.89 from 63.20, we get −5.69. This is the mean difference that is presented in column 9; it indicates that the average patient lost 5.69 kg more in the topiramate arm than in the placebo arm.
At the extreme right, in the forest plot, the first horizontal line displays the summary data for this study. The little dot on the horizontal line corresponds to the −5.69 mean difference that was stated in column 9. How do we know that the dot indicates −5.69? We look at the x-axis and its division marks, right at the bottom. The x-axis shows values of −5 and −10 to the left and 5 and 10 to the right. Values to the left favor the experimental group, meaning that topiramate patients lost more weight than the placebo patients did. Values to the right favor the control group, indicating that the control patients lost more weight.
Column 9 presents the 95% CI around the value −5.69. We see that the 95% CI is −20.11 to 8.73 (the values can be verified, should we wish to do so, using an online 95% CI calculator for the difference between means). The right end of the horizontal line representing this study corresponds to a value of 8.73, the upper bound of the CI. The left end is supposed to extend to −20.11, but because the x-axis at the bottom stops at −10, the left end of this line ends in an arrowhead that tells us that the line goes out of the picture in the direction of the arrow.
The 95% CI for this study (column 9) includes the value 0. This tells us that although topiramate was associated with substantially greater weight loss than placebo, the difference between groups did not reach statistical significance at the .05 level. The nonsignificance is also evident from the plot: the horizontal line corresponding to this study extends on both sides of the zero difference (shown on the x-axis) vertical line that runs from the top to the bottom of the plot. Because the zero difference vertical line runs through the horizontal confidence interval line, we conclude that “zero difference between groups” is also a possibility for the population that is represented by the data.
The 95% CI is also very wide; in fact, the horizontal line is longer for this study than for any other study in the plot. The extreme width of the 95% CI indicates that the value of the mean difference between topiramate and placebo is very imprecise in this study; the true value for the population (with 95% confidence) can lie anywhere along this very long line. Because the mean difference is imprecise, the weight assigned to this study is very small, just 2.4% (column 8). The dot on the horizontal line is actually a square. The area of the square indicates the weight assigned to the study. Because the square is so small that it seems no larger than a dot, we understand from the plot as well as from the number in column 8 that the weight assigned to the study is small.
The column heading above the horizontal lines in the plot states “weighted” mean difference. We have already seen that the mean difference is indicated by the position of the square on the horizontal line and that the weight is indicated by the size of the square. The abbreviation “IV” in the column heading for the plot stands for inverse variance, indicating that weights were assigned by the inverse variance method; that is, the greater the variance in the data, the smaller the weight assigned to the mean difference.13 Greater variance is indicated by greater width of the 95% CI. The column heading above the plot also refers to “random effects.” This will be addressed in a later section.
Study Data in the Forest Plot: 2
The second study in the upper forest plot in Figure 1 is listed as Roy Chengappa et al, 2007. In this study, 32 patients received topiramate and 14 received placebo (this is because patients were randomized 2:1, and not 1:1, as is conventionally done). The topiramate patients lost a mean of 1.49 kg and the placebo patients gained a mean of 2.72 kg; so the mean difference between groups is (−1.49) – (2.72), or −4.21 kg. The mean difference and the 95% CI are presented in numbers in column 9 and visually in the plot.
Three points are immediately apparent. The first point is that the entire horizontal line for this study lies in the “favors experimental” territory to the left of the vertical line. This indicates that “no difference” between groups is not a likely possibility for the population mean. This conclusion is also evident from the values for the 95% CI; the upper and lower bounds are both negative, indicating that the entire confidence interval is below 0. In other words, the difference between the topiramate and placebo groups was statistically significant in this study.
The second point is that the CI line for this study is much shorter than that of the Afshar et al, 2009 study. The implication is that the mean difference value identified in the Roy Chengappa et al study is more precise than that in the Afshar et al study. We can now appreciate why the Roy Chengappa study receives a higher weight (12.6%; column 8) and why the square that represents the mean difference in the Roy Chengappa study is larger in size.
The last point is that the values for the mean are very much smaller in this study than in the Afshar et al study. In fact, the mean values for all the other studies, as well, are far smaller than those reported by Afshar et al. The explanation is that Afshar et al reported study endpoint scores whereas the other studies reported endpoint vs baseline change scores. Actual body weight at study endpoint is a much larger number than change in body weight across the course of an RCT.
Endpoint scores and change scores are strikingly different in meaning as well as in value. However, considering that randomization usually makes groups closely similar at baseline, the between-groups difference in mean endpoint scores is likely to be very similar to the between-groups difference in mean change scores. Combining the mean difference in endpoint and change scores is therefore permissible.19
As a final note in this section, readers are invited to look at the Narula et al, 2010 data in the lower forest plot in Figure 1. This study has the narrowest 95% CI in the plot and hence earns the highest weight (28.4%), represented by the largest square in the plot.
Meta-Analysis Results in the Forest Plot
In the 2 previous sections, we examined representations of the source study data that comprised the raw data in the meta-analysis. In this section, we examine the findings in the meta-analysis.
Let us again examine the first forest plot in Figure 1. Toward the bottom, in the first column, we see a row with the heading “Subtotal.” This should more correctly read “Total.” This is the most important row in the forest plot; it is the row that presents the findings of the meta-analysis. We see in this row that the meta-analysis pooled data from a total of 176 topiramate patients and 151 placebo patients and that the 100% WMD was −3.14 (95% CI, −5.55 to −0.73). The numbers 176, 151, and 100.0 are simple totals of the numbers above, in the respective columns.
The WMD, −3.14, is the weighted, pooled estimate for the mean difference in body weight outcomes between topiramate and placebo groups in the 8 studies in this plot (so the heading for column 9 is correct, at least for this row). We conclude that, in these RCTs, relative to placebo, topiramate was associated with a mean weight loss of 3.14 kg. Because the entire 95% CI lies below 0 (the lower and upper bounds of the CI are both negative), we conclude that the pooled estimate (−3.14 kg) for the mean difference represents a statistically significant difference. Note that it is equally correct to use either MD or WMD to describe this pooled estimate.13
The diamond in the plot that lies at the extreme right of the meta-analysis results row presents the same results visually. The center of the diamond corresponds to the value −3.14 on the x-axis, and the left and right ends of the diamond correspond to the lower (−5.55) and upper (−0.73) bounds of the 95% CI. Because the entire diamond lies to the left of the “no difference between groups” vertical line, we conclude that the finding “favoring experimental” is statistically significant. The lowest row in this plot also expresses the statistical significance: for the “test for overall effect,” P = .01.
Heterogeneity, Subgroup Analysis, and Sensitivity Analysis
There is 1 more row in the forest plot that needs to be explained, and this is the second to last row. This row presents information about heterogeneity. In the first forest plot in Figure 1, we see in this row that there was very substantial statistical heterogeneity in the meta-analysis; the P value was < .00001 and the I2 value was 86%. What this means is briefly explained.
The results of studies that go into a meta-analysis can never be identical, if at least because of random variation. However, the results can be different also because studies differ in sample selection criteria, drugs and doses, rating instruments, follow-up duration, and other important clinical and methodological ways. All of these differences may produce what is known as statistical heterogeneity.
Statistical heterogeneity is formally assessed in meta-analysis, and the assessment informs us (a) whether or not the heterogeneity is statistically significant and (b) how large the heterogeneity (due to differences among study results) is. The magnitude of heterogeneity is described by the I2 statistic. This statistic tells us the percentage of the variability in the pooled estimate that is due to heterogeneity rather than to sampling error or chance.19 As a rule of thumb, heterogeneity is sometimes described as being low when I2 is less than 50%, moderate when I2 is 50%-75%, and high when I2 is greater than 75%. Other thresholds are also described.
Here is an example that will help the reader understand statistical heterogeneity. A hypothetical meta-analysis found that, relative to placebo, antipsychotic drugs were associated with an increased risk of extrapyramidal symptoms (EPS); heterogeneity associated with this finding was high. When the neuroleptic drug studies and the atypical antipsychotic drug studies were separately meta-analyzed, heterogeneity was found to be low in both meta-analyses, and only the neuroleptic drugs were associated with an elevated risk of EPS.
From this example, we see that high heterogeneity may arise from a subgroup effect. Authors may therefore plan subgroup analyses in advance, if they expect heterogeneity, or even if they merely wish to explore findings in subgroups of interest. Or, they may conduct exploratory subgroup analyses after discovering that heterogeneity is high, in order to identify the source of heterogeneity. Examples of subgroup analyses are those that are conducted separately in studies of younger and older patients, in studies of neuroleptics and atypical antipsychotic drugs, in studies of clozapine and other antipsychotics, in studies that used low doses and high doses of medication, in studies with short and long durations of follow-up, and so on. Subgroup analyses of this nature can also be used to understand what study characteristics influence the pooled estimate. Ideally, if this is the purpose of subgroup analysis, the analysis should be planned before the results of the meta-analysis are known, and there should be a scientific reason for planning to perform the specified subgroup analysis.
High heterogeneity could also arise from the biasing effect of 1 or more outlying studies. So sensitivity analyses may need to be conducted, repeating the meta-analysis with 1 or more studies omitted, to determine whether heterogeneity disappears with the omission of these studies. Sensitivity analysis, including preplanned sensitivity analysis, is also used to assess how robust the results of the meta-analysis are to other factors, such as studies that are rated to be at high risk of bias, or studies that are unusual in one or more regards. Finally, meta-regression analysis (described later) may also help identify the source of heterogeneity.
Heterogeneity is difficult to identify when the number of studies is small or when the pooled sample size is small. As a final note in this section, the square root of the “tau squared” value in the heterogeneity row is the SD of the pooled estimate. In the first forest plot in Figure 1, tau squared is 8.56. The square root of this number is 2.93. So we conclude that the SD of the pooled estimate, −3.14, is 2.93. We don’ t need to pay attention to this SD because we already have the 95% CI for −3.14, stated in column 9 and shown visually in the plot. The CI, like the SD, is a measure of variation. Readers are referred to Deeks et al19 for a more detailed discussion on heterogeneity.
Fixed Effect and Random Effects Meta-Analysis
In meta-analysis, a fixed effect model assumes that the population value of the outcome that is being assessed is the same in all the studies (so effect is a singular noun) and that if there are differences in the outcomes across studies, the differences are due to chance. In other words, the assumption is that there is no statistical heterogeneity. In contrast, a random effects model assumes that the true outcome is not the same in all studies; that is, that there is more than one true outcome (so effects is a plural noun). In such a situation, differences across studies are due to random factors as well as to study-related factors that create significant heterogeneity. The meta-analysis team must therefore choose whether to perform a fixed effect or a random effects analysis to estimate a single true value or the average of several true values.
Fixed and random effects models give the same result when there is no heterogeneity; that is, when I2 = 0. When I2 is greater than 0, the 95% CI around the random effects pooled estimate will be wider than that around a fixed effect pooled estimate. This means that random effects models are more conservative; that is, less likely to result in statistical significance.
Random effects models tend to weight studies more equally. This can be problematic if small studies with outlying results bias outcomes. There are many different methods for random effects meta-analysis; the DerSimonian and Laird method is one that is commonly used. However, this method may yield false-positive results when heterogeneity is high and the number of studies is small. A further discussion on fixed and random effects meta-analysis is available elsewhere.19,20
Meta-Analysis for SMD and RR/OR Values
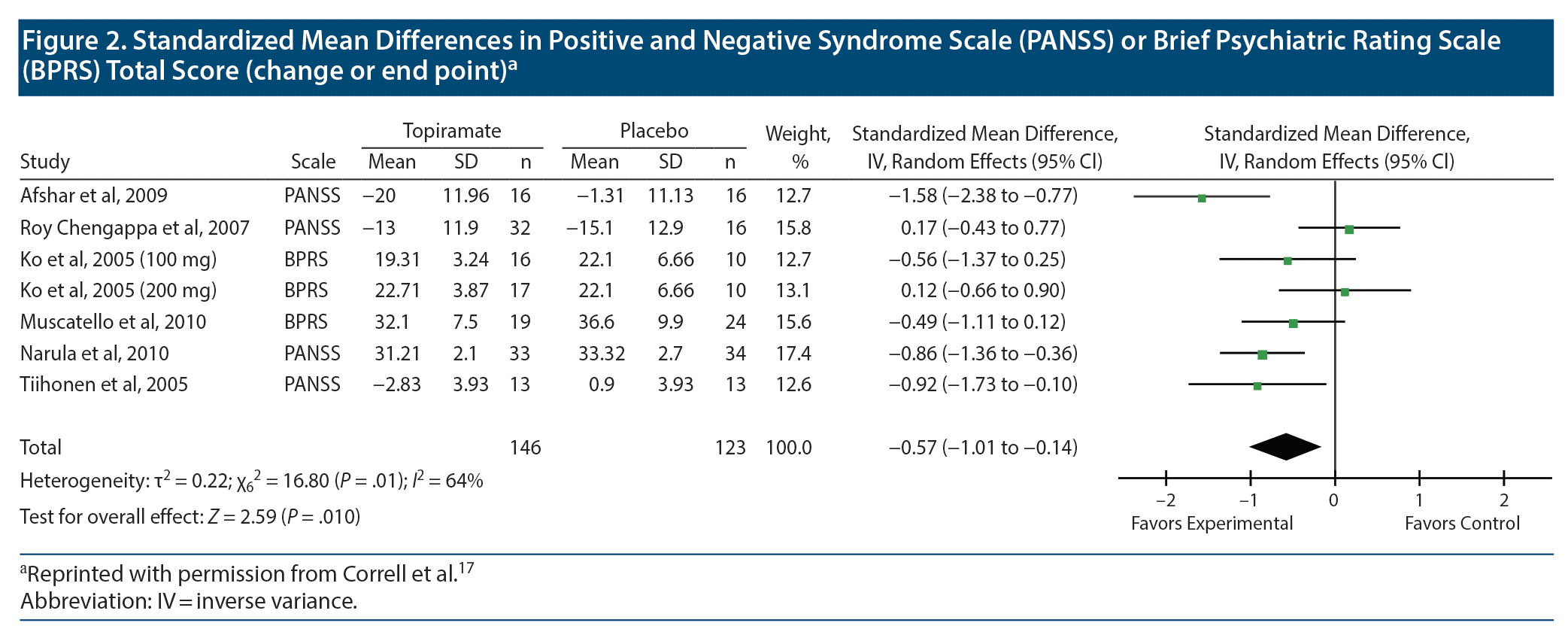
Let us now look at Figure 2, which presents meta-analysis results for psychopathology ratings. This figure has an extra column; it names the rating scale that was used in each study. Because different studies used different rating scales, the mean difference is no longer an appropriate statistic to be averaged in meta-analysis; it needs to be converted into an SMD, as was explained in an earlier article.13
The SMD for each study is the mean difference for the study divided by the pooled SD. To understand this, let us examine the data in Figure 2 for the Afshar et al study. The mean difference for topiramate vs placebo is (−20.0) – (−1.31); that is, −18.69. If we wish, we can use an online calculator to determine the value of the pooled SD, or, because the sample size is equal in the 2 groups, we can mathematically average the SD values and use the result, 11.55, as a crude estimate of the pooled SD (may the gods of pooled SDs pardon the sacrilege). When we divide −18.69 by 11.55, we get −1.62, which is not far from the value of −1.58 presented by the authors in the SMD (95% CI) column.
Note that we do not actually need to perform all these calculations to understand the data in the forest plot. These explanations are provided only to help the reader understand what the numbers mean and how they were obtained.
In all other regards, what is presented in Figure 2 is interpreted in exactly the same manner as was explained for Figure 1. Readers may note that the horizontal lines (95% CIs) are all of approximately the same width, which is why all the studies received approximately the same weight in the summary estimate (represented by squares of approximately the same area, in the plot). The conclusion is that topiramate reduces psychopathology ratings by slightly more than half an SD; the exact value is −0.57. The finding is statistically significant, as seen (a) from the 95% CI, (b) from the location of the diamond in the plot, and (c) from the test for overall effect (last row).
Forest plots are presented for RRs and ORs, as well. There are only a couple of important ways in which these plots differ from the plots shown in Figure 1 and Figure 2. One is that the data for individual studies present category data, such as number (percentage) of patients who responded, remitted, or had an adverse effect, instead of mean (SD) data. Another is that the vertical line of no difference has an x-axis value of 1, not 0, because an RR (or OR) of 1 represents “no difference” between groups.
Forest Plot: Curiosities and Mistakes
Observant readers would notice something unusual in Figure 1 and Figure 2. In each of the 3 plots, there are 2 rows for Ko et al, 2005. In this study, as we see from the author name column, the authors studied 2 doses of topiramate: 100 mg and 200 mg. The mean, SD, and n columns present different data for the 2 doses. However, the mean, SD, and n columns present identical data for the placebo columns. This is so for all 3 forest plots.
How can this be? Did the authors represent the same patients twice, in the placebo column? That is, were there 16 patients who received the 100 mg dose, 17 patients who received the 200 mg dose, and 10 patients who received placebo? If so, the double representation of the placebo group is unacceptable; the same analysis cannot have the same patients counted twice, inflating the total value of n for the placebo column. Reassuringly, the text of Correll et al17 explains that the authors divided the control group into two, assigning one half to each dose of topiramate.
Another issue is not so easily resolved. In Figure 2, for some studies the means are negative for both topiramate and placebo groups, and for some studies the means are positive for both groups. It’s not a case where values are close to 0 and where values may therefore lie on either side of 0; most of the mean values are fairly large. So what’s happening here?
As can be guessed from the title of this figure, the negative values represent a decrease from baseline in psychopathology ratings, and (most of) the positive values represent endpoint psychopathology ratings. As explained in an earlier section, combining mean differences of change scores and mean differences of endpoint scores is permissible when the summary statistic is the MD. However, when the summary statistic is an SMD, this is discouraged. The reason is that the SDs used in the standardization reflect constructs that differ between endpoint and change scores.19 There are ways of addressing situations such as this, none of which is satisfactory.21 Considering that the authors17 did not state what they did in their meta-analysis, it may be assumed that they took no steps and that, in consequence, the meta-analysis presented in Figure 2 contains errors.
Publication Bias
There is no assurance that all studies that are conducted on a particular subject will find their way into print and be discovered through a systematic search. Small studies with statistically nonsignificant outcomes are especially likely to suffer from a “file drawer” effect; that is, the results lie unpublished because authors assign low priority to preparing the manuscript for publication, or because editors are not enthusiastic about publishing small studies with unexciting findings. Industry-driven studies with nonsignificant or unfavorable results are especially likely to remain unpublished because of the obvious conflict of interest.
A good search strategy can reduce the risk that eligible studies are missed. However, there is no way of knowing whether unregistered studies that have been completed lie unpublished. One way of identifying the possible presence of publication bias is to look for asymmetry in a funnel plot. A funnel plot is a scatter plot with the effect size plotted on the x-axis and a measure of study precision plotted on the y-axis.
The funnel plot is best interpreted visually, though tests, such as the Egger test, are available for the purpose. It is difficult, though, to draw conclusions from a funnel plot when the number of studies is small, usually < 10. Asymmetry in a funnel plot does not necessarily confirm publication bias; other interpretations are also possible. The trim and fill method may be used to adjust for publication bias.22 However, this method may perform poorly if there is heterogeneity. For a further discussion, readers are referred to Sterne et al23 and Page et al.24
Meta-Analysis vs RCTs, and the Limitations of Meta-Analysis
A single, large, well-designed, well-conducted, and well-analyzed RCT is logically the pinnacle of the evidence pyramid. However, it is uncommon for such RCTs to be available or for any RCT to be above criticism. In any case, such RCTs often have narrow subject selection criteria, and so their findings cannot easily be generalized to the population. This is why it is widely held that meta-analysis is the highest level of evidence. Readers may however note that meta-analyses may also have major shortcomings.25,26
A special shortcoming of meta-analysis is the GIGO, or “garbage in, garbage out,” effect.5 On the one hand, a strength of meta-analysis is that it embraces diversity through the inclusion of a wide range of studies; therefore, the results are more easily generalized. On the other hand, embracing diversity could result in the inclusion of studies that are methodologically poor. Even worse, studies with untrustworthy data may be included; many such studies are being published, these days, from certain parts of the world. When the studies entered into a meta-analysis are of dubious quality, the results of the meta-analysis are also dubious.
Different meta-analyses, conducted at much the same time, may arrive at different conclusions, based on what studies were included and how the analyses were performed. For example, meta-analyses published in 2013 suggested that depression and diabetes mellitus each increased the risk of the other27,28 but also that neither increased the risk of the other.29 In a similar vein, 4 meta-analyses on the efficacy of baclofen in alcoholic patients were performed in widely different ways and obtained widely different conclusions.30
As a final note here, meta-analysis is conceptually easy to understand, and free statistical programs for meta-analysis are available. Conducting meta-analysis also requires less effort than conducting an original study from scratch. These reasons can tempt teams with insufficient knowledge and experience to undertake and publish meta-analyses. Mistakes made by such teams may not be apparent. Mistakes can also occur when meta-analyses are conducted by teams who are not fluent in the language of the studies from which they extract data. Finally, the selection of studies for meta-analysis may be poor when authors are knowledgeable about meta-analysis but do not know much about the field that they are investigating. This happens when teams function as meta-analysis factories that work on whatever opportunities they see.
Meta-Regression Analysis
Subgroup analysis, described earlier, is one method for determining whether study characteristics explain heterogeneity or the value of the summary estimate. Meta-regression analysis is another method. Meta-regression is conducted in exactly the same way as linear regression; the dependent variable is the study estimate (eg, MD or SMD), and the independent variables are the study characteristics (eg, low vs high dose studies, short- vs long-term trials). As with ordinary meta-analysis, studies in meta-regression receive weights that are based on the precision of their estimates. Thus, larger studies tend to receive higher weights.
An advantage of meta-regression analysis is that it can simultaneously model the effects of different study characteristics. A disadvantage is that, as with regression, at least 10 studies are desirable for each study characteristic that is examined. So, if the effects of high vs low dose studies and studies with older vs younger subjects are examined in meta-regression, because 2 study characteristics are examined, there should be at least 20 studies with the required data. If the number of studies is smaller, then there is an increase in the risk of overfitting and of false-positive results.
Readers are reminded that a statistically significant association, identified in meta-regression, does not prove that a cause-effect relationship exists. The role of confounding needs to be considered, much as it is in ordinary regression.19
Pooled Analysis
A pooled analysis is not the same as meta-analysis. In a pooled analysis, individual participant data from 2 or more nearly identical studies are put together and analyzed as though they were obtained from a single study. If this sounds like heresy, it is not. In multicenter studies, the same study protocol is executed at different sites and the data are pooled. In a pooled analysis, much the same is done except that the study protocols are nominally different. Usually, such identical or nearly identical studies would have been conducted by pharmaceutical companies for regulatory purposes, and the pooled analysis is to generate one more paper that gives more visibility to the new drug.
Pooled analyses may also examine the data from perspectives that were not addressed in the original analyses. Pooled analyses treat the data as though all data were obtained from the same study.31
Individual Participant Data Meta-Analysis
Individual participant data meta-analysis requires the authors of the meta-analysis to obtain individual participant data from the authors of the source studies. The data so obtained can be processed in different ways, but in all ways the original clustering of participants is retained; that is, the data continue to be treated as originating from different studies. There are many advantages of individual participant data meta-analysis over conventional meta-analysis. For example, the authors of the meta-analysis can conduct the meta-analysis on a set of participant characteristics that are similar across studies, and the statistical methods can be standardized across studies. One limitation of this kind of meta-analysis is that it is resource intensive for the meta-analysis team as well as for the source study authors who need to supply the data. Another limitation is that individual participant data may not be available for all source studies. A detailed discussion on the subject was provided by Riley and Lambert.32
Network Meta-Analysis
We have so far examined meta-analysis from the perspective of comparing 2 groups, such as drug and placebo. These are A vs B comparisons. Consider the situation where we have studies on A vs B, B vs C, C vs D, A vs D, and so on. However, we do not have studies for all pairwise comparisons. Situations of this nature can be examined through network (also known as multiple treatment comparisons) meta-analysis. This is a more complex procedure, involves direct and indirect comparisons, and provides estimates for all possible pairwise comparisons and estimates of the ranking and hierarchy of findings.33,34 Network meta-analysis has been used, for example, to compare 21 antidepressant35 and 32 antipsychotic36 drugs. Reading a network meta-analysis requires some additional understanding of the concepts involved and of the manner in which the results are presented.33,34
Conclusions
This article explained meta-analysis largely from the perspective of RCTs. Meta-analysis can also be conducted on cohort studies, case-control studies, and epidemiologic data. Although there must necessarily be differences in the ways in which such meta-analyses are conducted and presented, the general principles are the same, and a reader who has understood this article should be able to read and reasonably well understand meta-analyses that are conducted with other research designs.
Readers may also note that, even with meta-analyses of RCTs, different authors may present their forest plots in different ways. Again, the concepts are the same, and so understanding what is presented should not pose difficulties.
It is hoped that the reader who has read and understood this article will now understand the need for meta-analysis, what meta-analysis is, how meta-analysis is performed, what technical terms used in meta-analysis mean, and, in short, how to read and understand a paper that presents the results of a meta-analysis.
Published online: October 6, 2020.
 Each month in his online column, Dr Andrade considers theoretical and practical ideas in clinical psychopharmacology with a view to update the knowledge and skills of medical practitioners who treat patients with psychiatric conditions.
Each month in his online column, Dr Andrade considers theoretical and practical ideas in clinical psychopharmacology with a view to update the knowledge and skills of medical practitioners who treat patients with psychiatric conditions.
Department of Clinical Psychopharmacology and Neurotoxicology, National Institute of Mental Health and Neurosciences, Bangalore, India ([email protected]).
Financial disclosure and more about Dr Andrade.
REFERENCES
1.Pfefferbaum A, Rosenbloom M, Deshmukh A, et al. Sex differences in the effects of alcohol on brain structure. Am J Psychiatry. 2001;158(2):188-197. PubMed CrossRef
2.Hommer D, Momenan R, Kaiser E, et al. Evidence for a gender-related effect of alcoholism on brain volumes. Am J Psychiatry. 2001;158(2):198-204. PubMed CrossRef
3.Rudorfer MV, Linnoila M, Potter WZ. Combined lithium and electroconvulsive therapy: pharmacokinetic and pharmacodynamic interactions. Convuls Ther. 1987;3(1):40-45. PubMed
4.el-Mallakh RS. Complications of concurrent lithium and electroconvulsive therapy: a review of clinical material and theoretical considerations. Biol Psychiatry. 1988;23(6):595-601. PubMed CrossRef
5.Streiner DL. Using meta-analysis in psychiatric research. Can J Psychiatry. 1991;36(5):357-362. PubMed CrossRef
6.Tharyan P. The relevance to meta-analysis, systematic reviews and the Cochrane Collaboration to clinical psychiatry. Indian J Psychiatry. 1998;40(2):135-148. PubMed
7.Smith ML, Glass GV. Meta-analysis of psychotherapy outcome studies. Am Psychol. 1977;32(9):752-760. PubMed CrossRef
8.Lau J, Antman EM, Jimenez-Silva J, et al. Cumulative meta-analysis of therapeutic trials for myocardial infarction. N Engl J Med. 1992;327(4):248-254. PubMed CrossRef
9.Andrade C, Kisely S, Monteiro I, et al. Antipsychotic augmentation with modafinil or armodafinil for negative symptoms of schizophrenia: systematic review and meta-analysis of randomized controlled trials. J Psychiatr Res. 2015;60:14-21. PubMed CrossRef
10.McIntyre RS, Carvalho IP, Lui LMW, et al. The effect of intravenous, intranasal, and oral ketamine in mood disorders: A meta-analysis. J Affect Disord. 2020;276:576-584. PubMed CrossRef
11.Shamseer L, Moher D, Clarke M, et al; PRISMA-P Group. Preferred Reporting Items for Systematic Review and Meta-Analysis Protocols (PRISMA-P) 2015: elaboration and explanation. BMJ. 2015;350:g7647. PubMed CrossRef
12.Higgins JPT, Savovic J, Page MJ, et al. Assessing risk of bias in a randomized trial. In: Higgins JPT, Thomas J, Chandler J, et al, eds. Cochrane Handbook for Systematic Reviews of Interventions. 2nd ed. Chicester, West Sussex, England: John Wiley & Sons; 2019:205-228.
13.Andrade C. Mean difference, standardized mean difference (SMD), and their use in meta-analysis: as simple as it gets. J Clin Psychiatry. 2020;81(5):20f13681.
14.Andrade C. Understanding relative risk, odds ratio, and related terms: as simple as it can get. J Clin Psychiatry. 2015;76(7):e857-e861. PubMed CrossRef
15.Andrade C. Why odds ratios can be tricky statistics: the case of finasteride, dutasteride, and sexual dysfunction. J Clin Psychiatry. 2018;79(6):18f12641. PubMed CrossRef
16.Andrade C. A primer on confidence intervals in psychopharmacology. J Clin Psychiatry. 2015;76(2):e228-e231. PubMed CrossRef
17.Correll CU, Maayan L, Kane J, et al. Efficacy for psychopathology and body weight and safety of topiramate-antipsychotic cotreatment in patients with schizophrenia spectrum disorders: results from a meta-analysis of randomized controlled trials. J Clin Psychiatry. 2016;77(6):e746-e756. PubMed CrossRef
18.Shah N, Andrade C. A simple rearrangement can improve visual understanding of a Forest plot. Indian J Psychiatry. 2015;57(3):313-314. PubMed CrossRef
19.Deeks JJ, Higgins JPT, Altman DG; on behalf of the Cochrane Statistical Methods Group. Analysing data and undertaking meta-analyses. In: Higgins JPT, Thomas J, Chandler J, et al, eds. Cochrane Handbook for Systematic Reviews of Interventions. 2nd ed. Chicester, West Sussex, England: John Wiley & Sons; 2019:241-284.
20.Serghiou S, Goodman SN. Random-effects meta-analysis: summarizing evidence with caveats. JAMA. 2019;321(3):301-302. PubMed CrossRef
21.Higgins JPT, Li T, Deeks JJ. Choosing effect measures and computing estimates of effect. In: Higgins JPT, Thomas J, Chandler J, et al, eds. Cochrane Handbook for Systematic Reviews of Interventions. 2nd ed. Chicester, West Sussex England: John Wiley & Sons; 2019:143-176.
22.Duval S, Tweedie R. Trim and fill: A simple funnel-plot-based method of testing and adjusting for publication bias in meta-analysis. Biometrics. 2000;56(2):455-463. PubMed CrossRef
23.Sterne JAC, Sutton AJ, Ioannidis JPA, et al. Recommendations for examining and interpreting funnel plot asymmetry in meta-analyses of randomised controlled trials. BMJ. 2011;343:d4002. PubMed CrossRef
24.Page MJ, Higgins JPT, Sterne JAC. Assessing risk of bias due to missing results in a synthesis. In: Higgins JPT, Thomas J, Chandler J, et al, eds. Cochrane Handbook for Systematic Reviews of Interventions. 2nd ed. Chicester, West Sussex, England: John Wiley & Sons; 2019:349-374.
25.Huf W, Kalcher K, Pail G, et al. Meta-analysis: fact or fiction? how to interpret meta-analyses. World J Biol Psychiatry. 2011;12(3):188-200. PubMed CrossRef
26.Berlin JA, Golub RM. Meta-analysis as evidence: building a better pyramid. JAMA. 2014;312(6):603-605. PubMed CrossRef
27.Rotella F, Mannucci E. Depression as a risk factor for diabetes: a meta-analysis of longitudinal studies. J Clin Psychiatry. 2013;74(1):31-37. PubMed CrossRef
28.Rotella F, Mannucci E. Diabetes mellitus as a risk factor for depression: a meta-analysis of longitudinal studies. Diabetes Res Clin Pract. 2013;99(2):98-104. PubMed CrossRef
29.Hasan SS, Clavarino AM, Mamun AA, et al. Population impact of depression either as a risk factor or consequence of type 2 diabetes in adults: a meta-analysis of longitudinal studies. Asian J Psychiatr. 2013;6(6):460-472. PubMed CrossRef
30.Andrade C. Individualized, high-dose baclofen for reduction in alcohol intake in persons with high levels of consumption. J Clin Psychiatry. 2020;81(4):20f13606. PubMed CrossRef
31.Blettner M, Sauerbrei W, Schlehofer B, et al. Traditional reviews, meta-analyses and pooled analyses in epidemiology. Int J Epidemiol. 1999;28(1):1-9. PubMed CrossRef
32.Riley RD, Lambert PC, Abo-Zaid G. Meta-analysis of individual participant data: rationale, conduct, and reporting. BMJ. 2010;340:c221. PubMed CrossRef
33.Chaimani A, Caldwell DM, Li T, et al. Undertaking network meta-analyses. In: Higgins JPT, Thomas J, Chandler J, et al, eds. Cochrane Handbook for Systematic Reviews of Interventions. 2nd ed. Chicester, West Sussex, England: John Wiley & Sons; 2019:285-320.
34.Mills EJ, Ioannidis JP, Thorlund K, et al. How to use an article reporting a multiple treatment comparison meta-analysis. JAMA. 2012;308(12):1246-1253. PubMed CrossRef
35.Cipriani A, Furukawa TA, Salanti G, et al. Comparative efficacy and acceptability of 21 antidepressant drugs for the acute treatment of adults with major depressive disorder: a systematic review and network meta-analysis. Lancet. 2018;391(10128):1357-1366. PubMed CrossRef
36.Huhn M, Nikolakopoulou A, Schneider-Thoma J, et al. Comparative efficacy and tolerability of 32 oral antipsychotics for the acute treatment of adults with multi-episode schizophrenia: a systematic review and network meta-analysis. Lancet. 2019;394(10202):939-951. PubMed CrossRef
This PDF is free for all visitors!