The fragility index (FI) has been recommended for use as an additional statistic when presenting the results of randomized controlled trials (RCTs). The FI in a completed RCT is the smallest number of subjects whose status needs to be changed, such as from nonresponder to responder, for a statistically significant finding to lose its statistical significance. A small FI suggests that a finding is fragile; a large FI suggests that the finding is robust. Whereas an FI value of 0-1 indicates extreme fragility, there is no cutoff to separate what is small and what is large for the FI. The FI is useful because it helps readers understand significant findings of an RCT in a different and more intuitive way. The FI has limitations. It can only be calculated in the context of an RCT, and only when binary outcomes are compared between 2 groups. It should not be calculated in nonrandomized studies, because it cannot be adjusted for the biasing effect of confounding variables, nor in time-to-event studies, because it cannot include the effect of time. Interpretation of the FI can be problematic when the number of subjects who drop out for unknown reasons is large. RCTs with small samples and RCTs in which the event of interest is rare tend to be fragile. However, the most important limitation of the FI is that it revolves around the much decried use of a statistical threshold (usually P < .05) for determining the significance of a study finding. At best, the FI complements the understanding of the results of an RCT with statistically significant findings for categorical outcomes. It should be used and interpreted in the context of other statistical information, including summary statistics, measures of effect size, and confidence intervals.

ABSTRACT
The fragility index (FI) has been recommended for use as an additional statistic when presenting the results of randomized controlled trials (RCTs). The FI in a completed RCT is the smallest number of subjects whose status needs to be changed, such as from nonresponder to responder, for a statistically significant finding to lose its statistical significance. A small FI suggests that a finding is fragile; a large FI suggests that the finding is robust. Whereas an FI value of 0-1 indicates extreme fragility, there is no cutoff to separate what is small and what is large for the FI. The FI is useful because it helps readers understand significant findings of an RCT in a different and more intuitive way. The FI has limitations. It can only be calculated in the context of an RCT, and only when binary outcomes are compared between 2 groups. It should not be calculated in nonrandomized studies, because it cannot be adjusted for the biasing effect of confounding variables, nor in time-to-event studies, because it cannot include the effect of time. Interpretation of the FI can be problematic when the number of subjects who drop out for unknown reasons is large. RCTs with small samples and RCTs in which the event of interest is rare tend to be fragile. However, the most important limitation of the FI is that it revolves around the much decried use of a statistical threshold (usually P < .05) for determining the significance of a study finding. At best, the FI complements the understanding of the results of an RCT with statistically significant findings for categorical outcomes. It should be used and interpreted in the context of other statistical information, including summary statistics, measures of effect size, and confidence intervals.
J Clin Psychiatry 2020;81(2):20f13334
To cite: Andrade C. The use and limitations of the fragility index in the interpretation of clinical trial findings. J Clin Psychiatry. 2020;81(2):20f13334.
To share: https://doi.org/10.4088/JCP.20f13334
© Copyright 2020 Physicians Postgraduate Press, Inc.
The fragility index (FI)1 was recently strongly recommended for use in all trauma and surgical randomized controlled trials (RCTs) to assist in optimal decision-making in patient care.2 The authors2 observed that the FI improves the interpretation of RCT findings, complements the P value, and helps identify less robust study results.
This article explains what the fragility index is and considers its use and limitations in the context of psychopharmacology and brain stimulation RCTs.
Two Recent RCTs
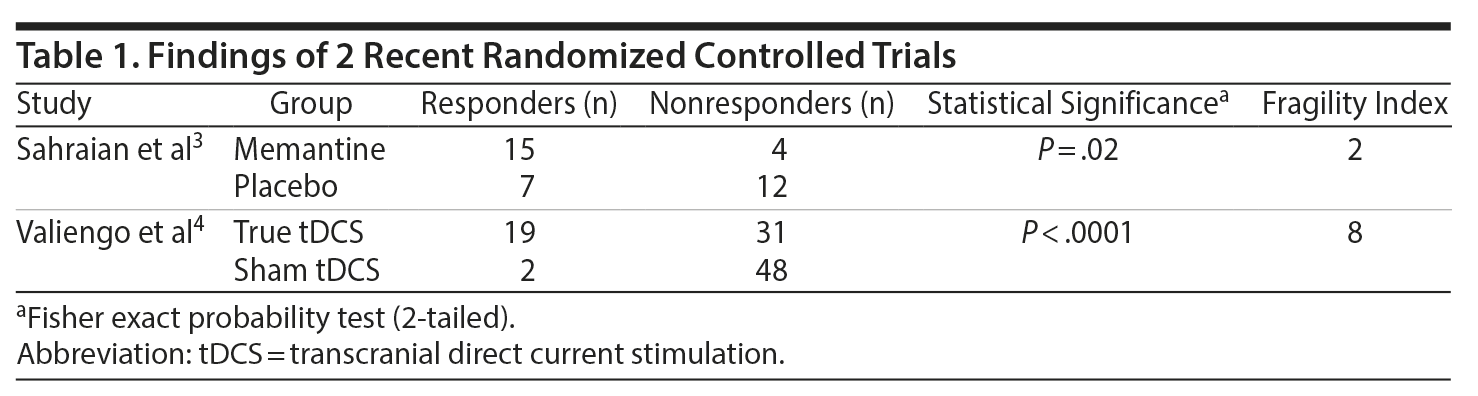
Sahraian et al3 presented a completer analysis of data from an RCT of memantine vs placebo as an adjuvant treatment for obsessive-compulsive symptoms in bipolar disorder (Table 1). They found that, at 16 weeks, 15 (78.9%) of 19 memantine patients vs only 7 (36.8%) of 19 placebo patients met response criteria, defined as 35% or greater decrease in scores on the Yale-Brown Obsessive Compulsive Scale. The advantage for memantine was statistically significant (Fisher exact probability [FEP] test, P = .02).
Valiengo et al4 presented an intent-to-treat analysis of data from an RCT of true vs sham transcranial direct current stimulation (tDCS) in patients with schizophrenia and prominent negative symptoms (Table 1). They found that, at 12 weeks, 19 (38%) of 50 tDCS patients vs only 2 (4%) of 50 sham tDCS patients met response criteria, defined as 20% or greater decrease in scores on the Positive and Negative Syndrome Scale, Negative Subscale. The advantage for tDCS was statistically significant (FEP < .0001).
Playing With the Numbers
Response thresholds define clinically meaningful improvement.5 In both of the examples presented in the previous section, the experimental intervention was associated with a response rate that was statistically significantly superior to the response rate associated with the control intervention. The response rates for experimental vs control intervention were 78.9% vs 36.8% in the first study3 and 38% vs 4% in the second4; in both studies, the superiority of the experimental intervention is visually impressive.
What happens if we make small adjustments to some of the numbers? In the first study,3 if 1 nonresponding control patient became a responder, the advantage for memantine over control treatment would change to 78.9% vs 42.1% and would remain statistically significant (FEP = .04). However, if 2 nonresponding control patients became responders, the advantage for memantine over control treatment would change to 78.9% vs 47.4% and would no longer be statistically significant (FEP = .09). If changing outcomes for just 2 control patients can negate the statistical significance of the finding, the advantage for memantine no longer appears as impressive as it did.
In the second study,4 however, it would take as many as 8 nonresponding control patients to shift from nonresponder to responder status for the memantine vs sham tDCS results (now 38% vs 20%) to lose statistical significance (FEP = .08). The findings of this study4 therefore appear to be somewhat more robust than that of the previous study.3
The Fragility Index
The number manipulations described in the previous section illustrate the concept of the fragility index. The FI in an RCT is the smallest number of subjects whose status needs to be changed, such as from nonresponder to responder, for a statistically significant outcome to lose its statistical significance.1,2 As illustrated in the calculations in the previous section, the FI is 2 for the Sahraian et al3 study and 8 for the Valiengo et al4 study (Table 1).
Small values of the FI indicate more fragile (or less robust) results, as the examples in the previous section show. The lowest meaningful value for the FI is 1. This means that the outcome of just 1 subject needs to be changed for a statistically significant result to lose its significance. The FI is always a positive integer and cannot be a fraction, for example between 0 and 1, because we cannot change the outcome status of one-half or one-third of a subject. An FI value of 0 may be assigned by fragility calculator software if the finding is not statistically significant to begin with. The FI cannot be negative because outcome status cannot be changed for a negative number of subjects.
Although lower values of the FI indicate greater fragility of the significant finding and higher values indicate greater robustness, there is no cutoff to define what is low and what is high.
Which Group?
Does it matter whether the change in outcome status is made in the experimental group or in the control group? Yes. For example, in the tDCS study,4 as already stated, 8 sham tDCS patients would need to change from nonresponder to responder status for the statistical significance to be lost; in contrast, 10 true tDCS patients would need to shift from responder to nonresponder status for the statistical significance to be lost.
So in which group should the change in status be examined to determine the FI? In this context, Walsh et al6 defined the FI with adjustment made to the numbers in the group with the smaller number of events. An online calculator (available at ClinCalc.com) also follows this procedure.
More Play With Numbers
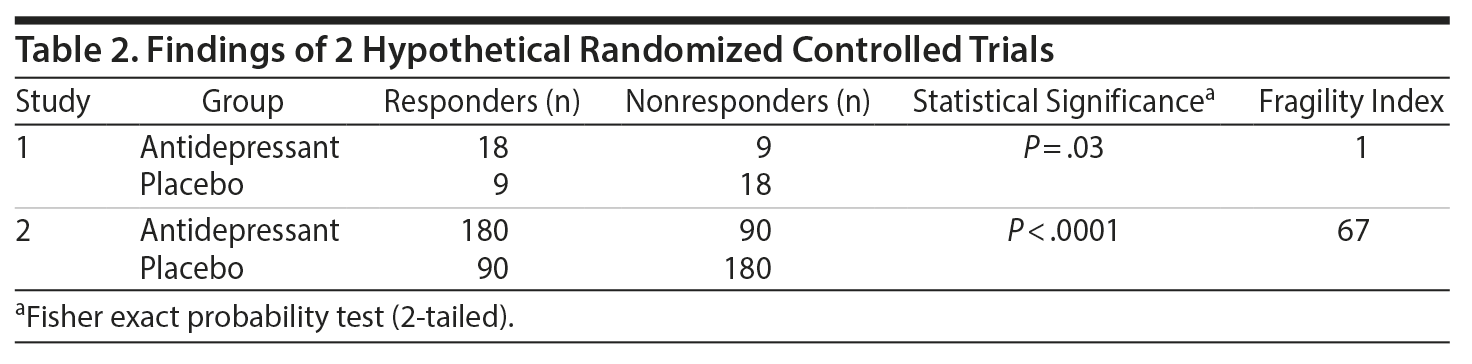
Consider the hypothetical RCT in which 54 depressed patients receive antidepressant drug (n = 27) or placebo (n = 27). At the end of the RCT, it is observed that there are 18 responders and 9 nonresponders in the antidepressant group and 9 responders and 18 nonresponders in the placebo group (Table 2). Eyeballing the data, it appears that the antidepressant is emphatically superior to placebo; after all, the findings with placebo are exactly the reverse of those with the antidepressant. The results are indeed statistically significant (FEP = .03). However, surprisingly, the FI for these data is 1, indicating that the finding is actually fragile.
What if the proportions remain the same but the numbers are larger? For example, what is the FI for 180 responders and 90 nonresponders in the antidepressant group vs 90 responders and 180 nonresponders in the placebo group (Table 2)? These results are also statistically significant (FEP < .0001), and the FI is 67. So, clearly, it is not just the value of the proportion but the size of the sample that also matters. To be more precise, for a given difference between groups, when the sample size is larger, the P value becomes smaller, and it is the smaller P value that is responsible for the larger value of the FI.
Digression: The P Value
RCT data are subjected to inferential statistical testing, which procedure ends with the estimation of a P value. The P value is the probability of obtaining a finding as or more extreme than that obtained in the study, were the hypothesis examined to be null in the population.7 What does this mean in simple English?
As an example, in the Valiengo et al4 RCT, the response rate of negative symptoms to true vs sham tDCS was 38% vs 4% (P < .0001). If the null hypothesis is true and there is actually no difference in the response of negative symptoms to true and sham tDCS, then P < .0001 means that the probability of obtaining an RCT result of 38% vs 4% (or a result that shows an even greater difference) is < .0001. So, if the null hypothesis is true, then a 35% vs 4% (or more extreme) result should occur by chance less often than once in 10,000 such identically performed RCTs. In other words, the 38% vs 4% result is very, very unlikely.
Given that only 1 and not 10,000 RCTs were performed, and given that this one RCT did obtain such an extremely unlikely result, we now have to choose between two possibilities: that the 38% vs 4% result was a gigantic fluke or that the null hypothesis is wrong. Conventionally, a P value of .05 (5%) is set as the threshold to decide that the finding is unlikely to be a fluke and that, consequently, the null hypothesis must be wrong. In other words, we use this .05 value as a cutoff to conclude that true tDCS is really associated with a higher response rate than sham tDCS with regard to attenuation of negative symptoms in schizophrenia.
It is important to note that the P value merely tells us how likely or unlikely the finding is. It tells us nothing whatsoever about how large the finding is.
In the Sahraian et al3 RCT, the response rate of obsessive-compulsive symptoms to memantine vs placebo was 78.9% vs 36.8% (P = .02). This means that if memantine is actually no better than placebo in the attenuation of obsessive-compulsive symptoms, then in only 2% of such identically performed RCTs would we obtain a result that is as or more striking than 78.9% vs 36.8%. Given that such an unlikely result was obtained when the study was performed for the first time, it is perhaps reasonable to apply the .05 threshold and conclude that the finding of the study was not a fluke and that memantine is truly superior to placebo for the attenuation of obsessive-compulsive symptoms. As a digression within a digression, this study had notable limitations, and the case for the use of memantine as an augmentation agent against obsessive-compulsive symptoms remains to be established.8
Usefulness of the Fragility Index
What the P value actually means is hardly ever properly understood by most readers and even by most researchers. Explaining the concept of P value is a lengthy procedure, as the preceding section shows. Understanding the concept is not easy; one may need to read the explanation more than once for the concept to sink in, and remembering what one has understood may require repeated visits to the explanation. So a strength, or rather the usefulness, of the FI is that it is very easily understood. No explanation is required to understand how fragile a finding is when one is told that the beautiful, statistically significant outcome of an RCT would be spoiled if just 2 placebo patients were to cross over from nonresponder to responder status (Table 1). Similarly, no explanation is required to understand how robust a result is when one is told that as many as 67 patients would need to cross over from nonresponder to responder status for an RCT outcome to lose its statistical significance (Table 2).
Note that the FI does not tell us what the P value means. It merely helps us understand the results of the study in a different and more intuitive way.
Limitations of the Fragility Index
The FI has many limitations.2,9 The FI can only be calculated for binary outcomes in a 2 ×— 2 contingency table, as in response vs nonresponse numbers in Group 1 vs Group 2 (Tables 1 and 2). It cannot be applied to continuous data, such as the magnitude by which a rating scale value is improved by a treatment. It also cannot be applied to the study of relationships between variables, such as is examined using correlation.
The FI should only be calculated for outcomes assessed in RCTs. In nonrandomized trials, confounding variables could influence the outcomes and hence introduce unknown biases in the value of the FI were the FI to be calculated. The FI is also inappropriate in time-to-event analyses where the outcome (eg, relapse) may be binary but where the time at which the event occurs (eg, earlier vs later) is also an important criterion.
The FI is unaffected when patients drop out of the RCT because of inefficacy or adverse events; these patients are appropriately classified as nonresponders. Interpretation of the FI can become problematic when a large number of patients drop out for unknown reasons, and especially so when such dropouts exceed the value of the FI. Classifying these patients as nonresponders may not necessarily be appropriate.
The FI, by its very definition, is closely related to the P value; so, P values just below the threshold for statistical significance are necessarily associated with smaller FI values than P values that are far below the threshold for significance. It is logical that a P value that is just below .05 is fragile; we do not need to calculate an FI to know this. So the FI does not really add new information; it merely helps us understand the result of the study in a different way. In this context, because RCTs that are based on an a priori estimation of sample size are likely to be powered to be just adequate to detect an expected difference, the findings of such RCTs may be fragile by design; in contrast, when the sample size is large, fragility is less likely, as evident from the examples in Table 2.
The most important limitation of the FI is that it reinforces the use of a P value (usually .05) that is set as the threshold for statistical significance. The P value is a continuous measure, and to introduce a cutoff to interpret the P value is considered by statisticians to be scientifically unsound.7 After all, why should a small change in P from, say, .049 to .051 dramatically change the way in which we view the outcome of a study? Furthermore, as explained in an earlier section, the P value tells us how likely or unlikely the finding is; it tells us nothing about the value of the finding in the population. In this regard, the use of a confidence interval provides a better understanding of the magnitude of the study results beyond that which is conveyed by a P value.7,10 The FI cannot and does not provide such information.
As a last point, RCTs are vulnerable to fragility when the outcome of interest is rare.
The Verdict
The FI has its uses and its limitations. What is the final verdict? A reasonable conclusion is that it should not be considered in isolation for interpretations and decision-making; however, it is a useful statistic to present in RCTs along with response rates, numbers needed to treat, 95% confidence intervals, P values, and such conventional statistics. The FI adds to one’s understanding of the results of an RCT with statistically significant results for categorical outcomes.
Parting Notes
The value of the FI will depend on the statistical test on which it was based. Thus, the value might vary slightly depending on whether contingency table testing was done using the χ2 test with continuity correction, the χ2 test without continuity correction or the FEP test. In this article, all calculations were based on the 2-tailed FEP test. The websites at which the FEP and FI values were calculated are stated in a note following this article. The online FI calculator employed the 2-tailed FEP test.
Published online: March 24, 2020
Additional information: The Fisher exact probability test calculations in this article were performed at GraphPad: https://www.graphpad.com/quickcalcs/contingency1/, and the Fragility Index calculations were performed at ClinCalc.com: https://clincalc.com/Stats/FragilityIndex.aspx.
 Each month in his online column, Dr Andrade considers theoretical and practical ideas in clinical psychopharmacology with a view to update the knowledge and skills of medical practitioners who treat patients with psychiatric conditions.
Each month in his online column, Dr Andrade considers theoretical and practical ideas in clinical psychopharmacology with a view to update the knowledge and skills of medical practitioners who treat patients with psychiatric conditions.
Department of Clinical Psychopharmacology and Neurotoxicology, National Institute of Mental Health and Neurosciences, Bangalore, India ([email protected]).
Financial disclosure and more about Dr Andrade.
REFERENCES
1.Walter SD. Statistical significance and fragility criteria for assessing a difference of two proportions. J Clin Epidemiol. 1991;44(12):1373-1378. PubMed CrossRef
2.Tignanelli CJ, Napolitano LM. The fragility index in randomized clinical trials as a means of optimizing patient care. JAMA Surg. 2019;154(1):74-79. PubMed CrossRef
3.Sahraian A, Jahromi LR, Ghanizadeh A, et al. Memantine as an adjuvant treatment for obsessive compulsive symptoms in manic phase of bipolar disorder: a randomized, double-blind, placebo-controlled clinical trial. J Clin Psychopharmacol. 2017;37(2):246-249. PubMed CrossRef
4.Valiengo LDCL, Goerigk S, Gordon PC, et al. Efficacy and safety of transcranial direct current stimulation for treating negative symptoms in schizophrenia: a randomized clinical trial [published online ahead of print October 16, 2019]. JAMA Psychiatry. doi:10.1001/jamapsychiatry.2019.3199. PubMed
5.Andrade C. Transcranial direct current stimulation for negative symptoms of schizophrenia: why the reader must choose a clinically relevant outcome. J Clin Psychiatry. 2020;81(1):20f13256. PubMed CrossRef
6.Walsh M, Srinathan SK, McAuley DF, et al. The statistical significance of randomized controlled trial results is frequently fragile: a case for a Fragility Index. J Clin Epidemiol. 2014;67(6):622-628. PubMed CrossRef
7.Andrade C. The P value and statistical significance: misunderstandings, explanations, challenges, and alternatives. Indian J Psychol Med. 2019;41(3):210-215. PubMed CrossRef
8.Andrade C. Augmentation with memantine in obsessive-compulsive disorder. J Clin Psychiatry. 2019;80(6):19f13163. PubMed CrossRef
9.Acuna SA, Sue-Chue-Lam C, Dossa F. The fragility index: P values reimagined, flaws and all. JAMA Surg. 2019;154(7):674. PubMed CrossRef
10.Andrade C. A primer on confidence intervals in psychopharmacology. J Clin Psychiatry. 2015;76(2):e228-e231. PubMed CrossRef
This PDF is free for all visitors!